Intersection of Two Linked Lists

Problem

Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.

For example, the following two linked lists begin to intersect at node c1:

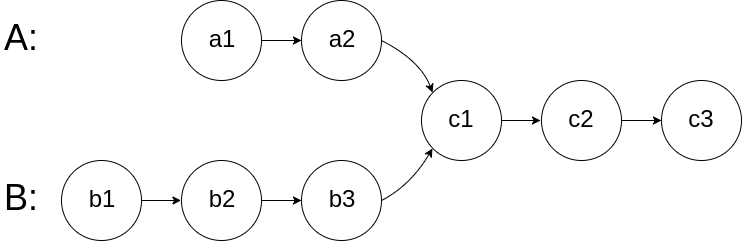
The test cases are generated such that there are no cycles anywhere in the entire linked structure.

Note that the linked lists must retain their original structure after the function returns.

Follow up: Could you write a solution that runs in O(m + n) time and use only O(1) memory?

Constraints

• The number of nodes of listA is in the m.
• The number of nodes of listB is in the n.
• 1 <= m, n <= 3 * 104
• 1 <= Node.val <= 105
• 0 <= skipA < m
• 0 <= skipB < n
• intersectVal is 0 if listA and listB do not intersect.
• intersectVal == listA[skipA] == listB[skipB] if listA and listB intersect.

Solution

The problem Intersection of Two Linked Lists can be solved either using Floyd’s cycle-finding algorithm or difference in node counts. First, it is possible to use Floyd’s cycle-finding algorithm by turning listA into a circular linked list. Once listA becomes a circular linked list, the problem becomes equivalent to finding a cycle in listB and its first element. If there is an intersection between listA and listB, there would be a cycle in listB with a size of m and start index of μ. In this case, the equation xμ + α _ m = xμ + β _ m would hold for integers α, β where xi represents ith element from the start of the list. If α = 0 and β = 1, than xμ = xμ + m would hold. In other words, if a fast pointer is first moved m steps from the start of the list while slow pointer sits at the start, and afterwards both pointers are moved one step each time, they will both be pointing at the start of the intersection / cycle after the μth step. On the contrary, if the process above is repeated and fast pointer reaches the end of the list, then it means that there are no cycle in listB which in turn means that there are no intersection between listA and listB.

Another implementation involves using the difference in node counts. If m = n, then 2 pointers starting from each list and moving by 1 node at a step would converge at the intersection if there is one. If m > n, then by starting first pointer at the (m - n)th node from the start of listA and second pointer from the start of listB, the same process can be repeated to find the intersection. This can be proven by the following. Size of listA can be represented as m = α + x and size of listB as n = β + x where x is the number of nodes after the intersection and α and β being the number of nodes before the intersection for listA and listB, respectively. As m - n = α - β, first pointer will be starting from (α - β)th node, having α + x - (α - β) = β + x nodes left to traverse through. Therefore, it is possible to find the intersection by starting first pointer at the (m - n)th node from the start of listA and second pointer from the start of listB and moving both pointers by β nodes.

Implementation (Floyd’s cycle-finding algorithm)

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution
{
  public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)
    {
        ListNode *head = headA;
        int loop_size;

        for (loop_size = 1; head->next != NULL; loop_size++)
            head = head->next;
        head->next = headA;

        ListNode *tortoise = headB;
        ListNode *hare = headB;

        int idx = 0;
        do
        {
            hare = hare->next;
            if (idx++ >= loop_size)
                tortoise = tortoise->next;
        } while (hare != NULL && tortoise != hare);

        head->next = NULL;
        return hare;
    }
};

Implementation (Difference in Node Counts)

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution
{
  public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)
    {
        ListNode *curA = headA;
        ListNode *curB = headB;

        while (curA != curB)
        {
            curA = curA == NULL ? headB : curA->next;
            curB = curB == NULL ? headA : curB->next;
        }

        return curA;
    }
};